一人麻雀和了確率計算アルゴリズムトップダウン vs ボトムアップ

トップダウンとボトムアップの定義を逆にしました。(2022/09/23追記)
実装例を追記しました。(2022/09/23追記)

このブログでは度々一人麻雀の和了確率を計算するアルゴリズムを取り上げてきました。ところでこのブログ以外でも一人麻雀の和了確率や期待値の計算方法を解説しているサイトがあります。

http://critter.sakura.ne.jp/ (critter 氏)
https://mahjong.ara.black/ (あら氏)
https://pystyle.info/mahjong-expected-value-in-mahjong/ (nekobean 氏)

これらのサイト、そしてこのブログは一人麻雀の和了確率や期待値を計算しているはずですが、すべて同じ値を計算できているのでしょうか？言い換えればこれらのサイトで用いられているアルゴリズムはすべて等価なのでしょうか？今回はこれらのアルゴリズムの関係を明らかにしたいと思います。なお先に結論を述べておくとすべて等価です。

先に言及したアルゴリズムに共通するのは手牌変化の木を探索するということです。手牌変化の木とは以下の図のように手牌の変化を木で表現したものです。なお、議論を簡単にするため以降では引いた牌に対してどの牌を捨てるかが事前に決まっているものとします。

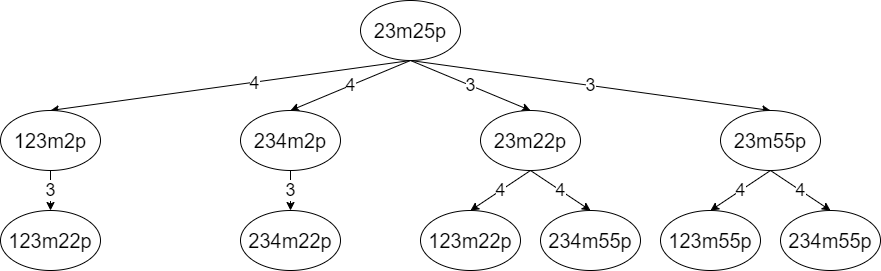
それぞれのアルゴリズムで求める値は次のように決定的に異なります。手牌変化の木の根を上としたときにそれらの値を上から下へ求めるか下から上へ求めるかによって、これらのアルゴリズムはトップダウンとボトムアップに分かれます。このブログでこれまで取り上げてきたアルゴリズムはトップダウンに、それ以外はボトムアップになります。

トップダウン: $t$ 巡目にノード $N$ の状態である確率 $q^{N}_t$ を求める。

ボトムアップ: $t$ 巡目にノード $N$ の状態であるとしたとき $t_{max}$ 巡目までに和了する確率 $p^{N}_t$ を求める。

簡単な問題を使って2つの違いを見ていきます。

$t = 0$ 巡目に $S$ 枚の牌がある。聴牌の手牌 $O$ から和了の手牌 $A$ に変化するための有効牌が $a$ 枚であるとする。 $t=t_{max}$ 巡目までに和了する確率を求めよ。

トップダウンの解法

次の連立確率漸化式を解く。

$\left\{ \begin{aligned} q^O_{t+1} &= \left( 1-\frac{a}{S-t} \right) q^O_t & q^O_0 &= 1 \\ q^A_{t+1} &= q^A_{t} + \frac{a}{S-t} q^O_t & q^A_0 &= 0 \end{aligned} \right. \tag{1}$

ボトムアップの解法

次の連立確率漸化式を解く。

$\left\{ \begin{aligned} p^O_t &= \left( 1-\frac{a}{S-t} \right) p^O_{t+1} + \frac{a}{S-t} p^A_{t+1} & p^O_{t_{max}} &= 0 \\ p^A_t &= p^A_{t+1} & p^A_{t_{max}} &= 1 \end{aligned} \right. \tag{2}$

どちらも似たような形式ですが行列で表現すると違いがはっきり見えます。

トップダウンの解法

$\begin{pmatrix} q^O_{t+1} \\ q^A_{t+1} \end{pmatrix} = \begin{pmatrix} 1-\frac{a}{S-t} & 0 \\ \frac{a}{S-t} & 1 \end{pmatrix} \begin{pmatrix} q^O_t \\ q^A_t \end{pmatrix} \tag{3}$

ボトムアップの解法

$\begin{pmatrix} p^O_t \\ p^A_t \end{pmatrix} = \begin{pmatrix} 1-\frac{a}{S-t} & \frac{a}{S-t} \\ 0 & 1 \end{pmatrix} \begin{pmatrix} p^O_{t+1} \\ p^A_{t+1} \end{pmatrix} \tag{4}$

(3)式と(4)式を見ると違いは2点あり、①時間発展の方向が互いに逆である②行列が互いに共役転置の関係にあることがわかります。計算過程は省略しますがこれらを解くと

$p^O_0 = q^A_{t_{max}} \tag{5}$

の関係が得られます。よってトップダウンとボトムアップのどちらでも同じ和了確率を得られます。

では手牌の変化の行先が複数の場合について考えてみます。例えば $O \rightarrow A$ の変化の他に $O \rightarrow B$ の変化がある場合、ボトムアップでは以下の連立確率漸化式を解きます。なおトップダウンについては https://tomohxx.github.io/mahjong-algorithm-book/ を参照してください。

$\left\{ \begin{aligned} p^O_t &= \left( 1-\frac{a+b}{S-t} \right) p^O_{t+1} + \frac{a}{S-t} p^A_{t+1} + \frac{b}{S-t} p^B_{t+1} & p^O_{t_{max}} &= 0 \\ p^A_t &= p^A_{t+1} & p^A_{t_{max}} &= 1 \\ p^B_t &= p^B_{t+1} & p^B_{t_{max}} &= 1 \end{aligned} \right. \tag{6}$

(6)式のように行先の分だけ項が増えます。ここまでに解説したボトムアップのアルゴリズムがおそらくcritter氏のアルゴリズムに相当すると思います。

ここで(2)式に戻ってこれを形式的に解いてみます。

$\begin{aligned} p^O_t &= \left( 1-\frac{a}{S-t} \right) p^O_{t+1} + \frac{a}{S-t} p^A_{t+1} \\ &= \left( 1-\frac{a}{S-t} \right) \left\{ \left(1-\frac{a}{S-t} \right) p^O_{t+2} + \frac{a}{S-t-1} p^A_{t+2} \right\} \\ &= \dots \\ &= \left( 1-\frac{a}{S-t} \right) \left( 1-\frac{a}{S-t-1} \right) \dots \left( 1-\frac{a}{S-t_{max}+1} \right) p^O_{t_{max}} \\ &\quad + \left( 1-\frac{a}{S-t} \right) \left( 1-\frac{a}{S-t-1} \right) \dots \left( 1-\frac{a}{S-t_{max}+2} \right) \frac{a}{S-t_{max}+1} p^A_{t_{max}} \\ &\quad + \left( 1-\frac{a}{S-t} \right) \left( 1-\frac{a}{S-t-1} \right) \dots \left( 1-\frac{a}{S-t_{max}+3} \right) \frac{a}{S-t_{max}+2} p^A_{t_{max}-1} \\ &\quad + \dots + \left( 1-\frac{a}{S-t} \right) \frac{a}{S-t-1} p^A_{t+2} + \frac{a}{S-t} p^A_{t+1} \\ &= \sum^{t_{max}-1}_{u=t} \left( 1-\frac{a}{S-t} \right) \left( 1-\frac{a}{S-t-1} \right) \dots \left( 1-\frac{a}{S-u+1} \right) \frac{a}{S-u} p^A_{u+1} \\ &= \sum^{t_{max}-1}_{u=t} \prod^{u-1}_{v=t} \left( 1-\frac{a}{S-v} \right) \frac{a}{S-t} p^A_{u+1} \end{aligned} \tag{7}$

念のため途中式を記載しました。さて(7)式は「 $t$ 巡目の和了確率は、 $u-1$ 巡目まで有効牌を引かず $u$ 巡目に有効牌を引く確率に $u+1$ 巡目の和了確率をかけたものを $u \in [t, t_{max}-1$ ]に渡って足したものである」と解釈できます。この(7)式を使うアルゴリズムがあら氏とnekobean氏のアルゴリズムに相当すると思います。

以上の議論から冒頭で言及した3つのサイトとこのブログで用いられたアルゴリズムはすべて等価であることが簡単には(厳密ではない)説明できました。

最後にどのアルゴリズムを使うべきか考えてみます。素朴に実装すれば計算量はどれも同じですが、ボトムアップでは途中のノードの和了確率をキャッシュする(メモ化再帰)ことで訪問するノード数を減らせるので計算速度を追求するならボトムアップを使うべきです。また(2)式と(7)式は等価ですが、(7)式はループカウンタの分変数が増えるので(2)式の方が実装が簡単だと思います。つまりcritter氏のアルゴリズムが一番おすすめです。

ここまで完全に机上の議論しかしてきませんでしたが、ボトムアップを実装したものがこちらです。

github.com

手替わりなし・シャンテン戻しなしの条件付きですが、5シャンテンまでなら1秒以下、6シャンテンでは10秒から20秒程度で和了確率を計算することができます。6シャンテンの計算はキャッシュを使うからこそできるのであって、キャッシュの使えないトップダウンでは時間がかかりすぎて事実上計算不可能です。というわけでボトムアップの優位性は明白です。また一般の5シャンテンや6シャンテンの高シャンテン数の手牌の和了確率を計算できるプログラムは他にないと思われます。なお高シャンテン数であっても対称性が高い特殊な手牌では以前から計算可能でした。