一人麻雀和了確率計算アルゴリズムまとめ

はじめに

今回はこれまでに議論してきた一人麻雀和了確率についていくつかの問題点・疑問点を解消します。

諸問題

存在確率と和了確率の再定義

前々回の記事のトップダウンとボトムアップの関係についての記述が不十分なので補足します。

tomohxx.hatenablog.com

$n-1$ 向聴の手牌を想定し、 $0$ から $n$ までの $n+1$ 個の状態(手牌)があるとします。状態間の遷移確率を表す以下の確率行列 $A_t$ を定義します。

$A_t = \begin{pmatrix} 1-\frac{a_0}{S-t} & 0 & \dots & 0 & 0 \\ \frac{a_0}{S-t} & 1-\frac{a_1}{S-t} & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & 1-\frac{a_{n-1}}{S-t} & 0 \\ 0 & 0 & \dots & \frac{a_{n-1}}{S-t} & 1-\frac{a_n}{S-t} \\ \end{pmatrix} \tag{1}$

$t = 0$ 巡目に $S$ 枚の牌があるとして $t = \tau$ 巡目に和了する確率は $\prod_{t=0}^{\tau-1} A_t$ の $(n, 0)$ 成分なので

$\displaystyle p = {}^t \boldsymbol{e}_n \left\{ \prod_{t=0}^{\tau-1} A_t \right\} \boldsymbol{e}_0 \tag{2}$

と書けます。なお行列とベクトルの添字は0始まりとします。また $\boldsymbol{e}$ は単位ベクトルです。これを計算する方法は2通りあり、① $\boldsymbol{e}_0$ に左から $A_t$ を繰り返し作用させる方法と② ${}^t \boldsymbol{e}_n$ に右から $A_t$ を繰り返し作用させる方法があります。①がトップダウンで②がボトムアップです。それぞれの方法は以下のように書けます。

トップダウン

$\begin{aligned} \boldsymbol{q}_{t+1} &= A_t \boldsymbol{q}_t \\ \boldsymbol{q}_0 &= \boldsymbol{e}_0 \end{aligned} \tag{3}$

ボトムアップ

$\begin{aligned} {}^t\boldsymbol{p}_t &= {}^t\boldsymbol{p}_{t+1} A_t \\ \boldsymbol{p}_\tau &= \boldsymbol{e}_n \end{aligned} \tag{4}$

このとき和了確率は

$p = {}^t\boldsymbol{p}_t \boldsymbol{q}_t = {}^t\boldsymbol{p}_0 \boldsymbol{e}_0 = {}^t\boldsymbol{e}_n \boldsymbol{q}_\tau \tag{5}$

です。

$\boldsymbol{q}_t$ は $t$ 巡目での状態の存在確率を表し、 $\boldsymbol{p}_t$ は $t$ 巡目での和了確率を表します。この例のように打牌を考えなければどちらの方法を使っても構いませんが、打牌を考える場合は各状態で和了確率が最大となる打牌を選択する必要があるのでボトムアップの方法しか使えません。

基底変換(パラメータ変換)

手牌変化が一通りではなく分岐する場合、確率行列として $A_t$ ではなく以下の $B_t$ を考えます。

$B_t = \begin{pmatrix} 1-\frac{a_0}{S-t} & 0 & \dots & 0 & 0 \\ \frac{b_0}{S-t} & 1-\frac{a_1}{S-t} & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & 1-\frac{a_{n-1}}{S-t} & 0 \\ 0 & 0 & \dots & \frac{b_{n-1}}{S-t} & 1-\frac{a_n}{S-t} \\ \end{pmatrix} \tag{6}$

これを $A_t$ と同じように扱いたいので以下の対角行列 $D_i$ を導入して基底を変換します。

$D_i = \begin{pmatrix} 1 & & & & \\ & \ddots & & \huge{0} & \\ & & \frac{b_i}{a_i} & & \\ & \huge{0} & & \ddots & \\ & & & & 1 \\ \end{pmatrix} \tag{7}$

ここで例えば $D^{-1}_i B_t D_i$ を考えると $i$ 行目は $A_t$ と同じになります。よって

$\displaystyle A_t = \left\{\prod_{i=0}^{n} D_i^{-1} \right\} B_t \left\{\prod_{i=0}^n D_i \right\} \tag{8}$

が成り立ちます。 $\boldsymbol{p}_t$ と $\boldsymbol{q}_t$ のかわりに $D_i$ によって基底を変換した $\boldsymbol{p'}_t$ と $\boldsymbol{q'}_t$ を使えば、手牌変化が一通りの場合と分岐する場合の確率の計算をほとんど同じようにできます。

手牌変化のグラフの正確な記述

前回の記事で手牌変化のグラフを導入しました。

tomohxx.hatenablog.com

一人麻雀和了確率は2次元確率DPで計算できます。それならばグラフは無向グラフではなくDAGとして記述すべきなような気がします。

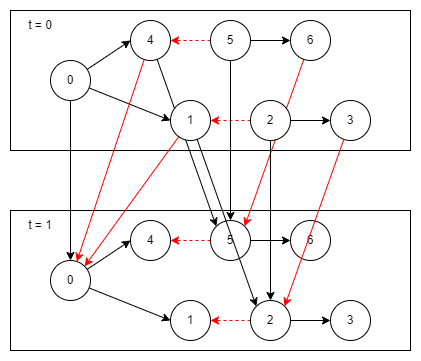
上の図では簡単のため2つの巡目しか記載していません。また矢印の色と線種については後述します。先述のように和了確率を求めるには各状態での和了確率を知らなければならないので、DPを使って計算する際は矢印の向きを逆向きにたどって各状態を訪問することになります。

緩和順

各状態での和了確率を表す漸化式は以下のようになります(前回の記事を参照)。

$p^v_t = \left\{ \begin{aligned} & p^v_{t+1} + \sum_{v' \in \mathrm{adj}(v)} \frac{e(v, v')}{S-t} (p^{v'}_{t+1} - p^v_{t+1}) & (v \in V_1) \\ & \max_{v' \in \mathrm{adj}(v)} \left\{ p^{v'}_t \right\} & (v \in V_2) \end{aligned} \right. \tag{9}$

添字が手牌方向と巡目方向と2つあるので、どちらをループの外側にするのかが問題になります。手牌変化のグラフを見ると巡目方向がトポロジカル順序になることがわかるので巡目をループの外側にすればよいことがわかります。ここで手牌変化のグラフから赤色の矢印がないとすると手牌方向もトポロジカル順序になります。赤色実線矢印は向聴戻し、赤色破線矢印は手替わりを表していると思ってください。この場合再帰的に手牌を探索しながら各巡目での和了確率を計算できるので、計算速度・メモリ効率ともに向上します。

辺の重み

辺の重みを巡目によらず固定としてよいのかは、和了確率を最大にする打牌をする場合2回以上同じ手牌を訪問しないので固定としてよいです。

不整合

手牌変化のグラフで辺の重みを巡目によらず固定すると、(6)式で $\sum_{v' \in \mathrm{adj}(v)} e(v, v') > S - t$ (ただし $p^{v'}_{t+1} > p^v_{t+1}$ )となる巡目で $p^v_t$ を確率として解釈できなくなります(前回の記事を参照)。このとき対応する存在確率は0になっているので和了確率は不定です。強いて言えば無効値として0や-1を割り当てるのがよいのかもしれません。あるいは捨てた牌は河ではなく山に戻るという仮定を受け入れてこの事態を回避するべきです。

得点期待値

和了確率ではなく得点期待値を求めたい場合、基本的には(9)式で和了確率 $p_t$ を得点期待値 $s_t$ に置き換えればよいです。ただし注意点が2点あります。1点目は得点は和了の状態に付属するのではなく聴牌から和了へ向かう辺に重みとして付属するということです。つまり辺は有効牌の枚数と得点の2種類の重みをもつことになります。2点目は和了の状態に到達したとして和了を宣言するか局を続行するか選択する必要があるということです。これらに注意して得点期待値を表す漸化式は以下のようになります。

$s^v_t = \left\{ \begin{aligned} & s^v_{t+1} + \sum_{v' \in \mathrm{adj}(v)} \frac{e(v, v')}{S-t} \left( \max \left\{f(v, v'),\ s^{v'}_{t+1} \right\} - s^v_{t+1} \right) & (v \in V_1) \\ & \max_{v' \in \mathrm{adj}(v)} \left\{ s^{v'}_t \right\} & (v \in V_2) \end{aligned} \right. \tag{10}$