tomohxxの日記

麻雀プログラミング

一人麻雀和了確率計算アルゴリズム グラフ探索

今回は前回の記事の続きです。
tomohxx.hatenablog.com

これまで手牌変化の木は与えられたものとして和了確率を求めてきました。基本的にシャンテン数が下がれば和了確率は上がると考えられるので、実装上は一方的にシャンテン数を下げる手牌変化の木を扱ってきました。しかし手替わりやシャンテン戻しを考慮すると、この手牌変化の木以外により高い和了確率を与える木が存在する可能性があります。つまり和了確率を最大にする手牌変化の木は自明ではありません。そこで手牌変化の木を構築することも含めた和了確率を計算するアルゴリズムを紹介します。

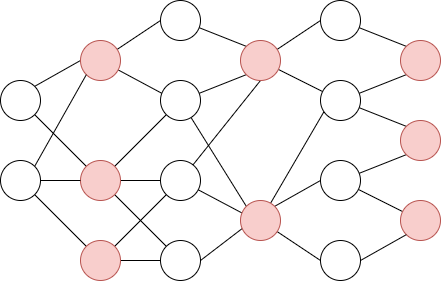
今回は手牌変化の木ではなく手牌変化のグラフを考えます。以下のような重み付き無向グラフ G(V_1, V_2, E)が与えられるとします。 V_1は13枚の手牌、 V_2は14枚の手牌を表し、異なる枚数の手牌を表す頂点同士は隣接するが同じ枚数を表す頂点同士は隣接しません。また辺 e(v_1, v_2) \in Eは13枚の手牌から14枚の手牌に変化するための牌の枚数を表します。なお、手牌の枚数をより一般に 3n+1枚、 3n+2枚としても構いません。

手牌変化のグラフのイメージ(白色の頂点が13枚の手牌、赤色の頂点が14枚の手牌を表す)

ここで和了確率を次のように定義します。

和了確率 p^v_t
t巡目に頂点 vにいるとして、別のある頂点を2回以上訪問しないで和了する確率

以下の連立確率漸化式を解いて和了確率を求めます。 \mathrm{adj}(v)は vの隣接する頂点の集合を得る演算です。
p^v_t = \left\{ \begin{aligned} & p^v_{t+1} + \sum_{v' \in \mathrm{adj}(v)} \frac{e(v, v')}{S-t} (p^{v'}_{t+1} - p^v_{t+1}) & (v \in V_1) \\ & \max_{v' \in \mathrm{adj}(v)} \left\{ p^{v'}_t \right\} & (v \in V_2) \end{aligned} \right. \tag{1}
初期条件は和了している手牌の集合を W \subset V_2として
p^v_t = \left\{ \begin{aligned} & 1 & (v \in W) \\ & 0 & (v \notin W) \end{aligned} \right. \quad (0 \le t \le t_{\mathrm{max}}) \tag{2}
です。

式の意味を簡単に説明します。まず(1)式の第2式は簡単で、手牌の枚数が14枚のときの和了確率をそこからある牌を捨てたときの和了確率の最大値とすることを意味します。次に(1)式の第1式ですが具体例を用いて説明します。現在頂点 v_0 \in V_1にいるとして頂点 v_1, v_2 \in V_2に隣接しているとします。前回の記事の要領で p^{v_1}_tを計算すると次のようになります。
\displaystyle p^{v_0}_t = \left( 1-\frac{e(v_0, v_1)+e(v_0, v_2)}{S-t} \right) p^{v_0}_{t+1} + \frac{e(v_0, v_1)}{S-t} p^{v_1}_{t+1} + \frac{e(v_0, v_2)}{S-t} p^{v_2}_{t+1} \tag{3}
これを変形すると
\displaystyle p^{v_0}_t = p^{v_0}_{t+1} + \frac{e(v_0, v_1)}{S-t} (p^{v_1}_{t+1} - p^{v_0}_{t+1}) + \frac{e(v_0, v_2)}{S-t} (p^{v_2}_{t+1} - p^{v_0}_{t+1}) \tag{4}
となるので、隣接する頂点数を一般化して(1)式の第1式になります。ここでもし p^{v_2}_{t+1} < p^{v_0}_{t+1}であれば v_0から v_2への変化を考えない方が和了確率が高くなると言えますが(1)式の第2式より p^{v_2}_{t+1} \ge p^{v_0}_{t+1}が保証されるので(1)式の第1式はそのままでよいことがわかります。つまり(1)式は不要牌をツモったときのツモ切りを内包していると言えます。

ところで巡目によって辺の重みが変化することは考えなくてよいのでしょうか？これは特定の計算条件の下では考える必要はありません。実は先の手牌変化のグラフの図には自己ループ e(v_1, v_1)が省略されています。これは自明な不要牌をツモ切りすることを意味していてその重みは S-t-\sum_{v' \in \mathrm{adj}(v)} e(v, v')で巡目によって変化します。自明な不要牌とは例えばタンヤオテンパイに対する字牌やホンイツに対する本命ではない色の数牌のような絶対にいらない牌です。自己ループを含めて辺の重みの合計が S-tであればよく、辺の重みの巡目依存性を自己ループに押し付けていることになります。逆に自明な不要牌が存在せず自己ループが存在しない場合(あらゆるツモを考慮して和了確率を計算する場合)(1)式は破綻することになります。*1*2

以上の議論を踏まえると和了確率を計算するには対象の手牌から変化可能な手牌の集合が必要でそれは手牌の全体集合ではないことがわかります。その集合の部分集合を得るのは簡単ですが、漏れなく効率的にこの集合の全要素を得る方法は現在検討中です。まあ、これについては和了確率とあまり関係ないような気がするので正直なところやる気が起きません。そこで、変化可能な手牌の集合を簡単に得られる場合として一色手の手牌の和了確率を計算してみました。
github.com
一色手の場合14枚の手牌のパターンは118800通り、13枚の手牌のパターンは93600通りなので時間的にも空間的にも計算可能な範囲です。

前述の通り、和了確率についてはもうやる気が起きないので新規に何かをするとしてもかなり先になると思います。あとこれまでに各所で公開したトップダウンの方法は今となっては人に勧められるものではなくなったので前回と今回の記事で扱ったボトムアップの方法に置き換えないといけないですね。面倒くさい……。

*1:一回捨てた牌は再び山に戻るという反則技の仮定を導入すれば自明な不要牌は考えなくてよくなります。

*2:仮に辺の重みの合計が S-tを超えたとしても p^{v'}_{t+1} = p^v_{t+1}であれば破綻しません。